Quantum Katas #2: Superposition

Intro⌗
If you read my last guide on basic quantum gates, you are familiar with the concept of superposition.
If not, let me briefly explain. A classical computer calculates on a system of binary "bits" that can either occupy the state \(0\) or \(1\), on or off.
A quantum computer on the other hand, uses qubits, or quantum bits which can occupy infinitely many states in between \(0\) and \(1\). When a qubit is in one of these "hybrid" states, we say that it is in superposition.
Consider the Bloch sphere below, which provides a visual reference for the state of a qubit.
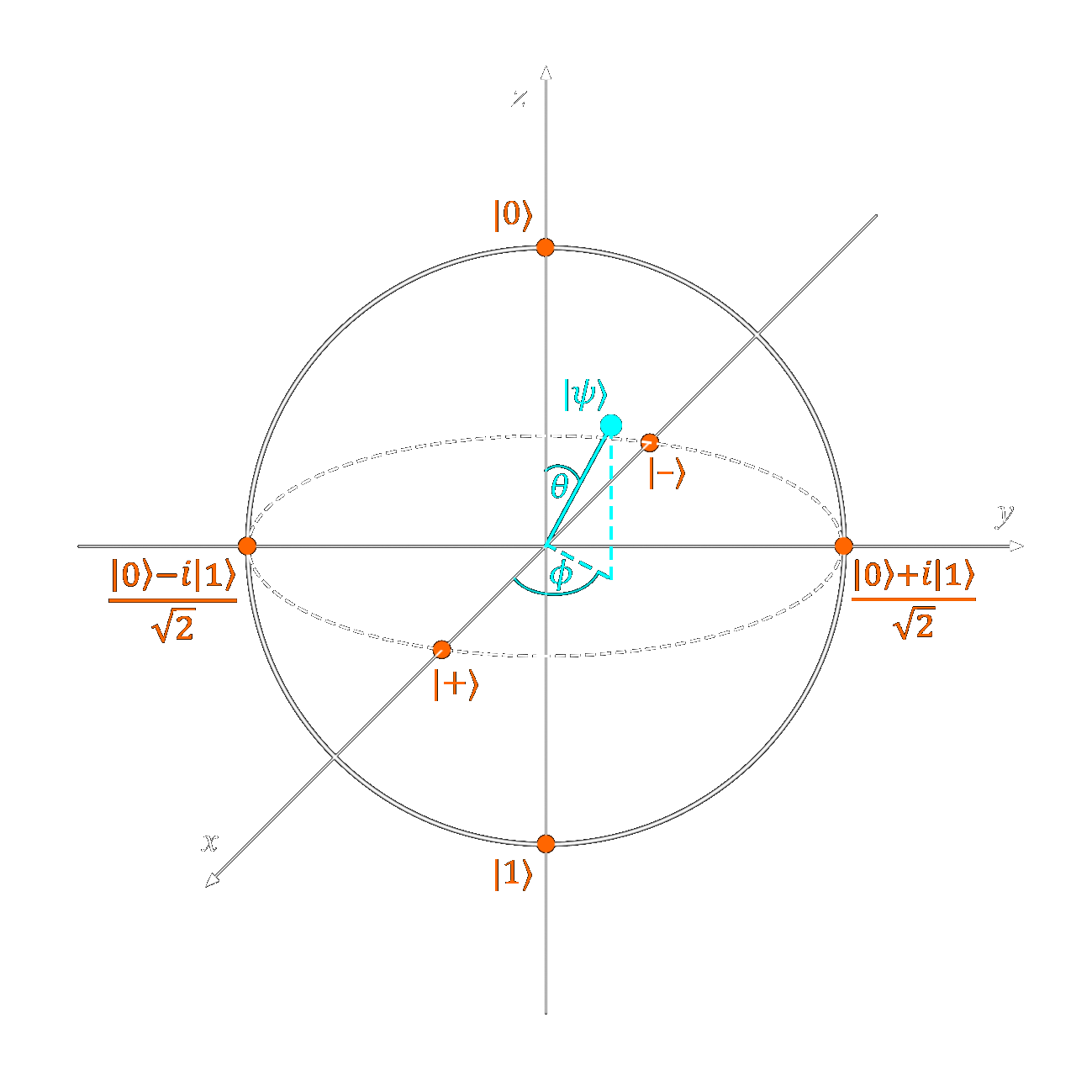
Like a classical bit, the qubit can take states \(0\) and \(1\), which are usually referred to as \(|0\rangle\) and \(|1\rangle\) when describing qubits.
We also see states \(|+\rangle\) and \(|-\rangle\), which represent a superposition halfway in between \(|0\rangle\) and \(|1\rangle\).
Finally we see the state vector \(|\Psi\rangle\), which can point to an arbitrary state on the surface of the bloch sphere. These arbitrary states are represented by angles \(\theta\) and \(\phi\).
The following programming challenges will have you manipulate qubits into various states of superposition. If you have not set up a Q# development environment, I suggest you take a look at my last post.
Task 1: Plus state⌗
As input, we are given a qubit in the \(|0\rangle\) state, and we need to output a qubit in the \(|+\rangle\) state.
Recall that the Hadamard gate maps qubits like so:
\(|0\rangle \rightarrow |+\rangle\) \(|1\rangle \rightarrow |-\rangle\)
Since we are only given qubits in the \(|0\rangle\) state, we can convert them to \(|+\rangle\) by simply applying the H() operation.
operation PlusState (q : Qubit) : Unit {
H(q);
}
Task 2: Minus state⌗
Like the previous task, we are given a qubit in the \(|0\rangle\) state, but now we must map it to the \(|-\rangle\) state.
Looking at the mappings for the Hadamard gate, we can see that applying H() to a qubit in the \(|1\rangle\) state will result in the \(|-\rangle\) state. We need to make use of the Pauli X gate to turn our \(|0\rangle\) states into \(|1\rangle\).
operation MinusState (q : Qubit) : Unit {
X(q);
H(q);
}
Task 3: Unequal superposition⌗
As I mentioned in the intro, the angles \(\phi\) and \(\theta\) on the Bloch sphere translate into an arbitrary superposition.
Let us consider the fact that we are trying to change the probability state of the qubit, which is represented by angle \(\theta\) between the \(|1\rangle\) state and the state vector \(|\Psi\rangle\).
Here we are tasked with putting the qubit into a superposition given by the angle \(\alpha\). A hint given in the comments reads:
Experiment with rotation gates from the Microsoft.Quantum.Intrinsic namespace.
Since we know that the probability state can be changed by rotating our state vector about the \(Y\) axis, we can leverage the Ry() operation.
operation UnequalSuperposition (q : Qubit, alpha : Double) : Unit is Adj {
Ry(2.0 * alpha, q);
}
Task 4: Superposition of all basis vectors on two qubits⌗
We finally reached our first 2-qubit gate of this kata.
Our goal is to take two qubits in state \(|00\rangle\) and convert them into the state
\[ \frac{|00\rangle + |01\rangle + |10\rangle + |11\rangle }{2}\]
Which is an equal probability of all possible outcomes of measurement.
This state is also represented by the tensor product of the two states
\[ |+\rangle \otimes |+\rangle \]
Since this superposition of qubits is represented by the tensor product of the qubits, we can simply use the H() gate to change both our qubits to the \(|+\rangle\) state.
operation AllBasisVectors_TwoQubits (qs : Qubit[]) : Unit {
H(qs[0]);
H(qs[1]);
}
Task 5: Superposition of basis vectors with phases⌗
Our goal in this task is to take two qubits in the \(|00\rangle\) state and convert them to the state
\[ \frac{|00\rangle + i|01\rangle - |10\rangle - i|11\rangle}{2} \]
This is another example of a \(n\) qubit state that can be broken down into the tensor product of \(n\) discreet states. In this case, the state above can be rewritten as
\[ \frac{|0\rangle - |1\rangle}{\sqrt{2}} \otimes \frac{|0\rangle + i|1\rangle}{\sqrt{2}} = |-\rangle \otimes |i\rangle\]
We already know how to put our qubits in these states! Take another look at the Bloch sphere to orient yourself. We are aiming for the \(|-\rangle\) and \(|i\rangle\) states, which both lie along the \(XY\) plane.
We can use the Hadamard gate to move our state vector to the \(|+\rangle\) state, and then use various rotations to get to the final states.
operation AllBasisVectorsWithPhases_TwoQubits (qs : Qubit[]) : Unit is Adj {
// Qubit 0 is taken into |+⟩ and then z-rotated into |-⟩.
H(qs[0]);
Z(qs[0]);
// Qubit 1 is taken into |+⟩ and then z-rotated into |i⟩.
H(qs[1]);
S(qs[1]);
}
Task 6: Bell state⌗
Again, we are getting an input of two qubits \(|00\rangle\). Our task is to create the bell state \(|\Phi^+\rangle\).
If you need a refresher on Bell states, please refer to my last post, where I explain the concept in more detail.
For now, we can simply recall that the \(|\Phi^+\rangle\) can be prepared by giving \(|00\rangle\) as an input to the Bell preparation circuit \(\beta\).
\[ |\beta_{00}\rangle \rightarrow |\Phi^+\rangle \]
Since we are already given the qubits in state \(|00\rangle\), we can easily prepare the desired bell state.
operation BellState (qs : Qubit[]) : Unit is Adj {
H(qs[0]);
CNOT(qs[0], qs[1]);
}
Task 7: All Bell states⌗
Here the input is the same as the last few tasks. This time however, we are also given an index, that corresponds to one of the four Bell states.
\( 0: |\Phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} \) \( 1: |\Phi^-\rangle = \frac{|00\rangle - |11\rangle}{\sqrt{2}} \) \( 2: |\Psi^+\rangle = \frac{|01\rangle + |10\rangle}{\sqrt{2}} \) \( 3: |\Psi^-\rangle = \frac{|01\rangle - |10\rangle}{\sqrt{2}} \)
We are given an input of \(|00\rangle\), so unless the input is 0, we will have to alter our qubits after preparing a bell state.
First let's consider the sign of the Bell state. If the index supplied is 1 or 3, it means we are preparing \(|\Psi^-\rangle\) or \(|\Phi^-\rangle\). Since our input \( |00\rangle\rightarrow |\Phi^+\rangle\), we need to flip the sign.
If you remember task 1.7 from my last post, this can be accomplished with the Z() operation.
The only thing left to check for now is if we need to go from \(|\Phi^{\pm}\rangle\) to \(|\Psi^{\pm}\rangle\)
Fill in the operation like so to complete the task.
operation AllBellStates (qs : Qubit[], index : Int) : Unit is Adj {
H(qs[0]);
CNOT(qs[0], qs[1]);
// now we have |00⟩ + |11⟩ - modify it based on index arg
if (index % 2 == 1) {
// negative phase
Z(qs[1]);
}
if (index / 2 == 1) {
X(qs[1]);
}
}
Task 8: Greenberger–Horne–Zeilinger state⌗
The Greenberger–Horne–Zeilinger state, or GHZ state, is a special, maximally entangled case of 3 or more qubits.
It takes the following form:
\[ GHZ_n = \frac{ \overbrace{|0...0\rangle}^{n} + \overbrace{|1...1\rangle}^{n} }{\sqrt{2}} \]
For example, a three qubit GHZ state is as follows
\[ GHZ_3 = \frac{|000\rangle + |111\rangle}{\sqrt{2}} \]
The observant may notice the similarity to the two qubit Bell state \(|\Phi^+\rangle\). In fact, the GHZ state can be prepared in a similar way.
Instead of preforming a Controlled NOT with the only two qubits, we can use the first qubit as the control and CNOT every additional qubit with it.
operation GHZ_State (qs : Qubit[]) : Unit {
H(qs[0]);
for(i in 1 .. Length(qs) - 1){
CNOT(qs[0], qs[i]);
}
}
In Q#, you can use the Rest() operation, which creates a copy of the input list removing the first element. This is the method shown in the solution, but you will have to add
open Microsoft.Quantum.Arrays;
to the top of your Tasks.qs file.
operation GHZ_State (qs : Qubit[]) : Unit {
H(qs[0]);
for(qubit in Rest(qs)){
CNOT(qs[0], qubit);
}
}
Task 9: Superposition of all basis vectors⌗
In this task, we need to create an equal superposition of \(n\) vectors. That will look like
\[ \overbrace{\frac{|0...0\rangle + ... + |1...1\rangle}{\sqrt{2^n}} }^{2^n \text{ permutations}} \]
For example:
\[ n =3 \rightarrow \frac{|000\rangle + |001\rangle + |010\rangle + |011\rangle + |100\rangle + |101\rangle + |110\rangle + |111\rangle}{\sqrt{2^3}} \]
This can be achieved by simply applying the Hadamard gate to every qubit. This is the same process we did for task 1.4, except with \(n\) qubits.
operation AllBasisVectorsSuperposition (qs : Qubit[]) : Unit is Adj {
for (q in qs) {
H(q);
}
}
Task 10. |00⟩ + |01⟩ + |10⟩ state⌗
Here we are tasked with putting two qubits into the state
\[ |\Psi\rangle = \frac{|00\rangle + |01\rangle + |10\rangle}{\sqrt{3}} \]
This means our 2 qubit state has a \(\frac{1}{3}\) chance of collapsing into each of the states \(|00\rangle, |01\rangle, |10\rangle\), with no chance of being in the state \(|11\rangle\)
I recommend taking a look at the stack exchange solution for more detail, but I will explain briefly here.
The first qubit in our input can be considered a control bit. For example, if our input is \(|10\rangle\), no action is needed and the state will measure \(|10\rangle\).
If the first qubit is \(|0\rangle\), we need to put our second qubit into the \(|+\rangle\) state, which will give an equal probability of measuring \(|00\rangle\) and \(|01\rangle\).
Now we can think of our qubit in the following form:
\[ |\Psi\rangle = \frac{\sqrt{2}}{\sqrt{3}}|0\rangle|+\rangle + \frac{1}{\sqrt{3}}|1\rangle|0\rangle\]
Which gives it a 66% chance of giving the plus state (which covers \(|01\rangle\) and \(|00\rangle)\) and a 33% chance of going straight to \(|10\rangle\). This neatly gives us our \(\frac{1}{3}\) chance of measuring any of the states.
How do we replicate this probability with our qubits? Well we want our first qubit to be in the \(|0\rangle\) state \(\frac{2}{3}\) of the time, so we have to adjust our probability amplitude.
Then for our conditional logic, we can use a "reverse controlled Hadamard", which will put the second qubit in the \(|+\rangle\) state if the first qubit is 0.
operation ThreeStates_TwoQubits (qs : Qubit[]) : Unit is Adj {
// Follow Niel's answer at https://quantumcomputing.stackexchange.com/a/2313/
// Rotate first qubit to (sqrt(2) |0⟩ + |1⟩) / sqrt(3) (task 1.4 from BasicGates kata)
let theta = ArcSin(1.0 / Sqrt(3.0));
Ry(2.0 * theta, qs[0]);
// Split the state sqrt(2) |0⟩ ⊗ |0⟩ into |00⟩ + |01⟩
(ControlledOnInt(0, H))([qs[0]], qs[1]);
}
Task 11: Superposition of |0...0⟩ and given bit string⌗
In this task, we must create a superposition of \(|0...0\rangle\) and an input given by a bit string.
The bit string:
- Has the same length as the qubit register
- Is guaranteed to start with a
1
For example, if the bit string was [true, false], the state we want to create would be
\[ \frac{|00\rangle + |10\rangle}{\sqrt{2}} \]
Here is a circuit that illustrates this on the input [true, false, true].
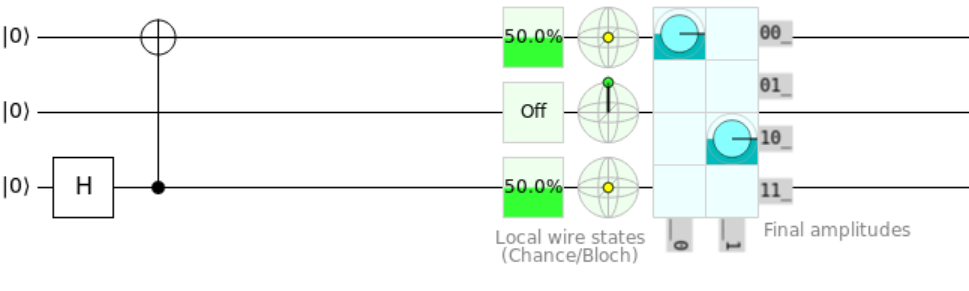
We apply the Hadamard gate to the first qubit, starting the superposition. For each following qubit, the CNOT gate is applied if the corresponding entry in the bit string is true.
The first qubit has a 50% chance of being \(|0\rangle\) or \(|1\rangle\). If it is zero, no more operations are applied, so the state \(|000\rangle\) is measured.
If the state of the first qubit (qs[0]) is one, all possible states that start with \(|0..\rangle\) are no longer possible.
In our above example, the second bit was false, meaning it will never get a NOT and will remain \(|0\rangle\). Hence, any state \(|.1.\rangle\) with 1 in the middle are not possible.
Similarly, a measurement of \(|100\rangle\) would be impossible since if the first qubit was \(|1\rangle\), the third qubit would have the NOT gate applied.
After eliminating the impossible measurements, the probability matrix gives us an equally probable output of \(|000\rangle\) and \(|101\rangle\).
Here I used the Length() function in a ranged for loop to check the value of the \(i^{th}\) bit in the input and apply CNOT accordingly.
operation ZeroAndBitstringSuperposition(qs : Qubit[], bits : Bool[]) : Unit is Adj{
// Hadamard first qubit
H(qs[0]);
// iterate through the bit string and CNOT to qubits corresponding to true bits
for (i in 1 .. Length(qs) - 1) {
if (bits[i]) {
CNOT(qs[0], qs[i]);
}
}
}
Task 12: Superposition of two bit strings⌗
In this task, we are given two arbitrary bit strings of length \(n\). For example if we had two input strings [false, true, false] and [false, false, true], we would create an equal superposition of like this:
\[ \frac{|010\rangle + |001\rangle}{\sqrt{2}} \]
The first step in completing this task is to find the spot where the two bitstrings "diverge".
By putting this bit into superposition, we splits our state into two distinct possible outcomes. Here is a helper function that returns the index of the first differing qubit:
function FindFirstDiff (bits1 : Bool[], bits2 : Bool[]) : Int {
mutable firstDiff = -1;
for (i in 0 .. Length(bits1) - 1) {
if (bits1[i] != bits2[i] and firstDiff == -1) {
set firstDiff = i;
}
}
return firstDiff;
}
Once we found where the strings diverge, we can apply the H() gate to it to create superposition. Next, we have to iterate through our bitstrings and put the qubits in their final state.
If the bit in both strings at index \(i\) are the same, we have two possibilities:
- They are both
false, meaning no action is needed. - They are both
true, and we need toNOTour qubit register at index \(i\)
If the bit in both strings at index \(i\) are different, we use the first different bit as a control, and CNOT the qubit at index \(i\).
If the first differing qubit measures as \(|1\rangle\), then the \(i^{th}\) qubit is flipped to \(|1\rangle\).
Then, if the first bitstring at index \(i\) is not equal to the value of the first different bit from the first string, we NOT the qubit at index \(i\).
The pseudocode above can be realized with the following operation:
operation TwoBitstringSuperposition (qs : Qubit[], bits1 : Bool[], bits2 : Bool[]) : Unit is Adj {
// find the index of the first bit at which the bit strings are different
let firstDiff = FindFirstDiff (bits1, bits2);
// Hadamard corresponding qubit to create superposition
H(qs[firstDiff]);
// iterate through the bit strings again setting the final state of qubits
for (i in 0 .. Length(qs) - 1) {
if (bits1[i] == bits2[i]) {
// if two bits are the same apply X or nothing
if (bits1[i]) {
X(qs[i]);
}
} else {
// if two bits are different, set their difference using CNOT
if (i > firstDiff) {
CNOT(qs[firstDiff], qs[i]);
if (bits1[i] != bits1[firstDiff]) {
X(qs[i]);
}
}
}
}
}
Task 13: Superposition of four bit strings⌗
This task is like the one above, except we must deal with 4 bitstrings, with \(N\) elements each.
Elements can be accessed like bits[i][j] where \(0 \lt i \lt 3\) and \(0 \lt j \lt N - 1 \).
First we can use the ApplyToEach() function to apply the Hadamard gate to each of the ancilla qubits to put them in the \(|+\rangle\) state.
Then we iterate through the rows and columns of our 2D array, touching each qubit. If bits[i][j] is true, we preform the following operation: (ControlledOnInt(i, X))(anc, qs[j]);
Then we have to iterate through each bitstring. If we are on bits[i] and \(i\) is odd, we do
(ControlledOnBitString(bits[i], X))(qs, anc[0]);
If it's even, we do
(ControlledOnBitString(bits[i], X))(qs, anc[1]);
Here is the implementation.
operation FourBitstringSuperposition (qs : Qubit[], bits : Bool[][]) : Unit is Adj {
let N = Length(qs);
using (anc = Qubit[2]) {
// Put two ancillas into equal superposition of 2-qubit basis states
ApplyToEachA(H, anc);
// Set up the right pattern on the main qubits with control on ancillas
for (i in 0 .. 3) {
for (j in 0 .. N - 1) {
if ((bits[i])[j]) {
(ControlledOnInt(i, X))(anc, qs[j]);
}
}
}
// Uncompute the ancillas, using patterns on main qubits as control
for (i in 0 .. 3) {
if (i % 2 == 1) {
(ControlledOnBitString(bits[i], X))(qs, anc[0]);
}
if (i / 2 == 1) {
(ControlledOnBitString(bits[i], X))(qs, anc[1]);
}
}
}
}
Task 14: W state on 2ᵏ qubits⌗
A W state is a state of \(N\) qubits that takes the following form:
\[ |W_N\rangle = \frac{\overbrace{|100...0\rangle + |010...0\rangle + ... + |00..01\rangle}^{N \text{ states}}}{\sqrt{N}} \]
In this task, we are challenged with creating the state \(|W_N\rangle\) where \(N = 2^k\).
We will implement a recursive operation to create the \(W\) state.
In this operation, our base case is when \(N = 1\), where the \(W\) state is trivially prepared. If we are in this state, we can apply X(qs[0]) and return.
If not, we must preform the following steps:
- Create new variable \(K = \frac{N}{2} \)
- Recursively call the function passing it
qs[0 .. K - 1]as input - Create an ancilla qubit and apply
H()to it - For every qubit from 0 to K - 1, do a controlled swap using the ancilla,
qs[i], andqs[i + K] - For every qubit from 0 to N - 1, preform a
CNOTwithqs[i]and the ancilla.
operation WState_PowerOfTwo (qs : Qubit[]) : Unit is Adj {
let N = Length(qs);
if (N == 1) {
// base of recursion: |1⟩
X(qs[0]);
}
else {
let K = N / 2;
// create W state on the first K qubits
WState_PowerOfTwo (qs[0 .. K - 1]);
// the next K qubits are in |0...0⟩ state
// allocate ancilla in |+⟩ state
using (anc = Qubit()) {
H(anc);
for (i in 0 .. K - 1) {
Controlled SWAP([anc], (qs[i], qs[i + K]));
}
for (i in K .. N - 1) {
CNOT(qs[i], anc);
}
}
}
}
Task 15: W state on arbitrary number of qubits⌗
Our task here is the same as in the previous, except now we cannot assume that \(N = 2^k\).
Again, we find the length of are qubit register using the Length() function.
Our base case for this recursive function is when \(N = 1\), where we can again preform X(qs[0]).
If we aren't at the base case, we want to preform a rotation on the first qubit to put it into the following state:
\[ \sqrt{\frac{N-1}{N}}|0\rangle + \frac{1}{\sqrt{N}}|1\rangle \]
We can accomplish this with an Ry() operation on the first qubit, rotating by \(2\theta\), where
\[ \theta = sin^{-1}\left(\frac{1}{\sqrt{N}}\right) \]
Then we preform a zero controlled recursive call of the same function. A zero controlled gate can be preformed by applying a standard controlled gate to a qubit who's state has been flipped.
This recursive loop will continue until we are at the base state, and where we will preform X(qs[0]) and reach our target state.
operation WState_Arbitrary (qs : Qubit[]) : Unit is Adj + Ctl {
let N = Length(qs);
if (N == 1) {
// base case of recursion: |1⟩
X(qs[0]);
}
else {
// |W_N⟩ = |0⟩|W_(N-1)⟩ + |1⟩|0...0⟩
// do a rotation on the first qubit to split it into |0⟩ and |1⟩ with proper weights
// |0⟩ -> sqrt((N-1)/N) |0⟩ + 1/sqrt(N) |1⟩
let theta = ArcSin(1.0 / Sqrt(IntAsDouble(N)));
Ry(2.0 * theta, qs[0]);
// do a zero-controlled W-state generation for qubits 1..N-1
X(qs[0]);
Controlled WState_Arbitrary (qs[0 .. 0], qs[1 .. N - 1]);
X(qs[0]);
}
}
Conclusion⌗
In this kata, we learned about the various special states and properties of quantum superposition, as well as some nontrivial implementations of these states with Q#.
As always, feel free to reach out with questions or feedback 😄